逆運動学

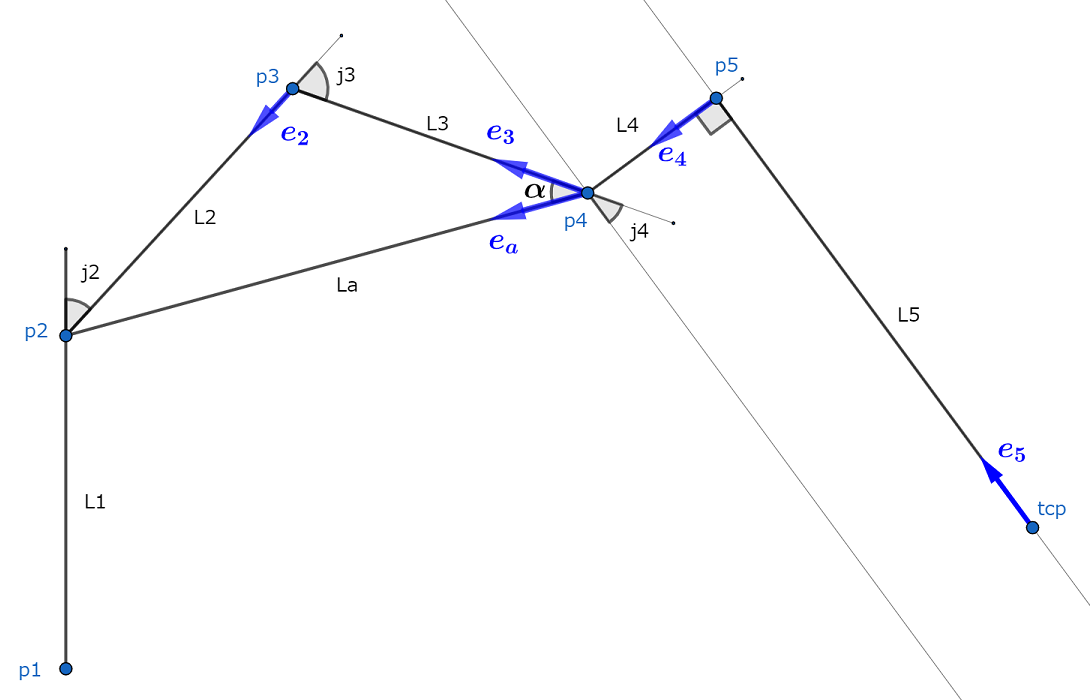
逆運動学は、手先の位置と姿勢(角度)から軸の角度を求めます。

\[\newcommand\v[1]{\boldsymbol{#1}} \newcommand\r[1]{\mathrm{#1}}\]

tcpからp5に向かう単位ベクトル \(\v{e_5}\) は

\[\begin{split}\begin{flalign} & \theta_2 = \pi - \theta \\ & \v{e_5} = (\cos \theta_2, \sin \theta_2) \end{flalign}\end{split}\]

p5の位置は

\[p5 = tcp + L5 \cdot \v{e_5}\]

p5からp4に向かう単位ベクトル \(\v{e_4}\) は

\[\v{e_4} = \r{rot}(\v{e_5}, \frac{\pi}{2})\]

p4の位置は

\[p4 = p5 + L4 \cdot \v{e_4}\]

p4とp2の距離を \(L_a\) とします。

\[L_a = \| p4 - p2 \|\]

三角形p2, p3, p4で、p4の角度を \(\alpha\) とすると、余弦定理から

\[\cos \alpha = \frac{L3^2 + L_a^2 - L2^2}{2 \cdot L3 \cdot L_a}\]

\(cos\) の逆関数 \(\arccos\) を使い

\[\alpha = \arccos (\cos \alpha)\]

p4からp2に向かう単位ベクトルを \(\v{e_a}\) とすると

\[\v{e_a} = \r{unit}(p2 - p4)\]

p4からp3に向かう単位ベクトル \(\v{e_3}\) は

\[\v{e_3} = \r{rot}(\v{e_a}, - \alpha)\]

p3の位置は

\[p3 = p4 + L3 \cdot \v{e_3}\]

p2, p3, p4, p5, tcpのすべての位置が分かったので、それぞれの軸の角度は容易に計算できます。

\[j1 = \arctan \frac{y}{x}\]

\[j2 = \arctan(p3 - p2) - \frac{\pi}{2}\]

\[j3 = \arctan(p4 - p3) - \arctan(p3 - p2)\]

\[j4 = \arctan(tcp - p5) - \arctan(p4 - p3)\]

\[j5 = \phi\]